Shape the Data, Shape the Thinking #2: Visualizing Statistical Aggregations

Summary statistics are essential, but we have to learn how to avoid major pitfalls

(This is part 2 of the series on the role of data transformation in data visualization. Part 1 was about Selection and Aggregation. Part 2 is about the numbers we can generate when we perform aggregations, their effect on interpretation, and the type of inferences we are allowed to make from these numbers).

In Part 1, I mentioned aggregation and explained that often, the data contained in the original table of a data set is “summarized” by aggregating all the items that have the same value for a selected attribute (or a set of attributes in more complex cases). What I didn’t mention is the fact that when we aggregate the numeric values, we have to choose a statistical function to decide how to turn multiple numbers into a single summary number.

In this post, I will keep using the same data set I introduced in Part 1 on vehicle collisions. Below is a snippet of the data table I that collects this information (with a subset of the attributes that are present in the whole data set.

Data table with information about vehicle collisions in New York City. The snippet shows only a subset of the attributes (columns) that are present in the whole data set.

When I aggregate the number of persons injured by zip code, I have to decide how to aggregate the numbers found within each zip code. While individual collisions will have a variable number of persons injured, I have to produce a summary number that represents something about the entire zip code area. Which number should I produce? For example, I could sum the values, compute the mean, or find the highest value. All of these are legitimate choices, but they also have direct consequences on 1) what information the reader will be able to extract and, more importantly, 2) what inferences I will be allowed to make. According to what number I use, some inferences will be valid, and some will not.

In this post, I will introduce some common types of statistical aggregates and discuss how each aggregate has relevant consequences on what we can infer from them. In particular, I will highlight how each type of number can generate faulty inferences and how to think about them effectively so that a) you will use them mindfully when creating your own visualizations (that is, you can anticipate and prevent potential interpretation problems from your readers) and b) you will be able to analyze other people’s visualization critically and assess the validity of what is presented to you. We will cover counts and sums, averages, and percent and ratios.

Counts and sums

Many visualizations display numbers that represent counting or summing values. In the vehicle collisions data set, one can count the number of collisions (by counting the number of rows since each row represents one collision) or sum the number of persons injured (by summing up the values found in each row regarding the number of persons injured in an accident).

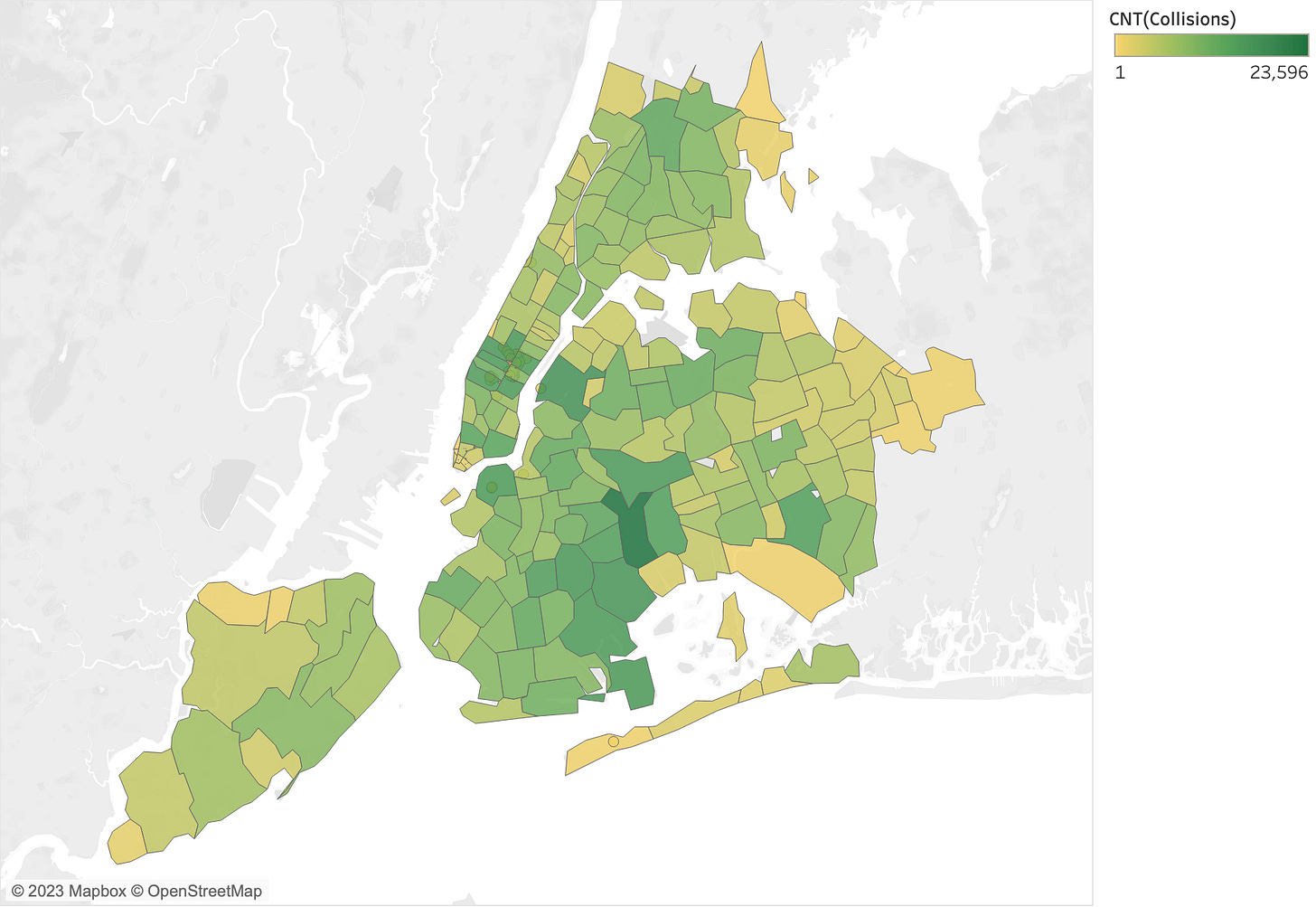
Counts and sums are very common and very powerful. We are interested in many things that involve counting and summing things up (e.g., in personal finance). However, whenever we use these quantities, we must be mindful of how they can be misleading once they are visualized. The first problem we will analyze is the base rate bias. The graph below depicts the number of collisions in different New York City zip codes.

Count the number of collisions in each zip code in New York City.

Looking at this chart, one may be tempted to conclude that the zip codes with darker areas are more dangerous than the others because they have a higher number of collisions. Our reasoning goes like this: more collisions imply more dangerous spots. But, upon reflection, one may realize that the number of collisions in a given area is influenced by how many vehicles there are in the area at any given time; therefore, areas that have a higher density of vehicles or areas that are just larger than others can have more collisions just because there are more vehicles around. The same problem exists when we compute the sum of injured persons in each borough. Since the number of persons injured depends on the number of collisions and the number of collisions depends on the number of vehicles circulating in the area, the sum is also subject to the same type of bias. In fact, when we look at the sum of persons injured in each zip code, we obtain the graph on the left below. But if instead of the sum, we compute the average number of persons injured per collision (the chart on the right), now we have a normalized number that does not depend on the number of vehicles and people in the area (except for a different problem I am going to introduce and describe below).

Sum of persons injured on the left and average number of persons injured on the right.

As you can see, the two graphs paint a different picture. With the graph on the right, it is more legitimate to draw inferences about how dangerous a given borough is because the numbers reflect more closely the likelihood of being involved in a dangerous accident if one is circulating in that area.

This problem exists every time we have an additive value, that is, when the number is generated by adding values together. Since the addition depends on the number of items that are added together, the numbers are sensitive to the frequency of items within each category. Above, I have shown an example with bar charts, but the same is true with any other chart that shows aggregated data. For example, you can have the same problem with maps or line charts when different regions, for maps, and points in time, for line charts, have different frequencies.

Averages

It is probably not an understatement to state that averages are the most used statistics in data communication ever. They are everywhere, from scientific papers to newspapers. An average tells us the central tendency of a set of numbers. However, as with any other summary, it necessarily hides useful information, and, as such, it can mislead in several ways.

The first problem with averages is that they hide the distribution of the data. When we read about averages, we tend to interpret them as coming from a distribution where the average is the most common value, and the values around it become increasingly unlikely as we move away from the average. But this interpretation is true only if the data behind these values is normally distributed, that is, if the distribution has the familiar bell shape. However, data sets can be distributed in many different ways, and the same average value can be obtained from data sets that have significantly different distributions.

The image below, from the paper “Beyond Bar and Line Graphs: Time for a New Data Presentation Paradigm,” describes the problem well.

Data with significantly different distributions look very similar to aggregated (see the bar graph associated with all of these distributions). Read the paper linked above for more details.

All the data sets on the right lead to very similar mean values, yet they look substantially different.

A subtler problem with averages arises when we compare average values coming from subsets (categories, regions, time intervals, etc.) with different underlying frequencies. Imagine we want to establish what are the most problematic zip codes by looking into the average number of persons injured in a collision. We can create a plot like the one on the left below, which depicts the top 30 zip codes using the average number of persons injured.

Average number of persons injured by zip code, on the left. Count of collisions on the right. Zip codes with high average values (the top ones) are not meaningful because the averages are calculated from too few data points (see corresponding frequency bars on the left).

Looking at the plot, we may readily conclude that the most dangerous zip codes are the ones found at the top of the list. The problem with this conclusion is that some averages are calculated from hundreds of thousands of collisions, whereas others are from just a handful. You can see this in the plot on the right, which depicts the number of collisions (frequency) behind the averages depicted on the left.

The ones calculated from just a handful of collisions are more prone to being very high or very low just because even a single extreme (low or high) value can have a much bigger impact on the average. In other words, while in this bar chart some values are very reliable, others are less reliable, and comparing them can lead to misleading conclusions. In general, averages calculated from a larger sample have less variability than those calculated from a smaller sample, and when we compare them, we have to take this discrepancy into account.

An interesting consequence of this effect is that when we observe average statistics (or even ratios and percentages) across several groups or entities, we should expect groups with a small frequency to display the highest and lowest values. In other words, we have to be careful not to overinterpret the presence of particularly low or high values in specific categories or areas. This is especially true in geographical visualizations, where some areas are often characterized by a lower frequency (e.g., sparser population). This effect is so important that a cognitive bias called “insensitivity to sample size” exists to capture this idea.

Percents and ratios

Out of all these summary statistics, percentages may be the most confusing and troublesome. Percentages are used in many ways in visualization, some useful and enlightening, and some confusing and misleading. Let me start with some useful uses of percentages.

One useful use is when the focus of our analysis and communicative intent is what is called a “part-to-whole” relationship. Often, we are more interested in how the proportion of certain categories differs between different entities. For example, using our running example, one can be interested in whether the main “contributing factors” behind a collision differ between different areas of New York, that is, are the types of collisions different between, say, Manhattan versus Brooklyn? This question can be analyzed through graphical depictions that focus on the proportion of each type across geographical regions, like the graph below.

Percent of top 5 “contributing factors” for each NYC borough. Percentages are useful to communicate information about “part-to-whole” relationships.

Another good use of percentages is when we transform frequencies into percentages to enable more direct comparisons between categories. We can use the same example above to make this clear. In order to answer the question above, I may be tempted to use a grouped bar chart like the one below, with the frequency of collisions mapped to bar length.

Frequency of collisions of the top 5 most contributing factors by NYC borough. Comparing bar length across boroughs does not give us information about how proportionally frequent a factor is within each borough.

This solution seems fine, but on a second look, you may realize that comparing the bars across the regions is not meaningful because different regions have different overall frequencies, so the length of the bars does not tell us what we want to know, which is how frequent a given type of collision is within a borough. A better way to pursue our initial question is to normalize the bars by converting counts into percent of collisions within each region. As you can see in the image below, where I applied this transformation (see the difference in the y-axis), it’s way easier to compare the composition of collision types across regions. A comparison of bar lengths between boroughs now gives us the information we need.

Proportion of contributing factors within each NYC borough. Since the vertical axis now corresponds to the percentage within each borough, comparing bar lengths across boroughs is meaningful in this graph.

In many other cases, percentages are very confusing. One of the biggest problems with percentages is that often it is not clear the percentage of what precisely the values indicate. For instance, the values can indicate the percent increase or decrease with respect to a common reference value or with respect to the previous point in time, and ambiguity between these two options can create a lot of confusion. One specific problem arises when percentages are calculated as change with respect to the previous point in time. The problem is that the same amount of percent increase or decrease can mean completely different quantities according to what quantity they refer to. For example, if my initial value is 100 and I have a 50% increase followed by a 50% decrease, I do not return to the initial value. A 50% increase brings me to 150, and the following 50% decrease brings me to 75, not 100.

Another problem with percentages is that they can mislead by showing big numbers about small quantities. A frequent kind of framing is when percentages are used to communicate the “improvement” of something. A given intervention or solution can produce an improvement of 50%, but if the original number is small, that improvement can be, in practice, insignificant.

There are many other ways in which percentages can mislead; too many to produce a complete catalog here. I suggest, though, to always ask, “percentage of what?” This question is crucial in order to identify problems. If you are designing a visualization based on percentages, please make it clear what percentage you are using and try to prevent misunderstanding that can stem from the use of percent values.

Conclusion

In this post, we covered summary statistics as an essential tool for data visualization. Without aggregation, we can’t communicate information effectively. However, aggregations come with a cost because they necessarily hide information. Here, I presented some common issues that stem from the use of counts and sums, averages, percentages and ratios. Covering every possible problem with aggregation is probably impossible; therefore, a good attitude for information consumers and designers is always to be alert to potential issues stemming from summarized data. Before concluding, I want to briefly mention that other forms of aggregation exist in addition to the ones I presented above. For example, often data values are transformed into rankings. Statistical measures of variability (dispersion) are also very important. But I decided to restrict myself to the ones presented above for brevity. If you have questions about these other forms of aggregation, I would be happy to provide more information.

—

P.s. If you enjoyed this post, please write a comment below. Let me know what you found insightful and if there is anything confusing you’d like me to explain. Also, I would appreciate it if you could share this post with others, especially on social media websites.